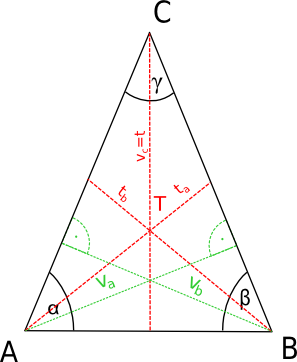
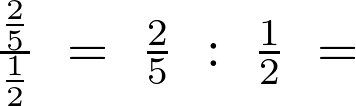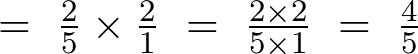Když mi bylo kolem 15 let, tak jsme si s kámošema říkali, „k čemu nám ta matika je, vždyť z toho co se učíme nebudeme nic potřebovat. Na co zlomky, procenta? Stačí, když si spočítám výplatu“, tak jsem byli hloupí. V tomto článku bych Vám chtěl ukázat, proč je matematika důležitá.

V patnácti jsem věděl ….. (nic) o tom jak to v životě chodí (navíc to bylo před revolucí 😉 ) a nedovedl jsem si představit situace, kdy se mi bude matematika hodit. Dnes už mám něco za sebou a můžu Vám s největší naléhavostí říct, že bez matematiky to nejde. A teď vám zkusím přiblížit několik situací, kdy se bez matematiky neobejdete.

Sčítání a odčítání

Začít můžeme u základních početních operací sčítání a odčítání. Možná tomu nebudete věřit, ale je spousta lidí co i pro sečtení 5+7 bere do ruky mobil a hledá kalkulačku. Nejen, že s tím ztrácí zbytečně spoustu času, ale navíc co až kalkulačka po ruce nebude?  Sčítání a odčítání z hlavy do 100 je nutnost a větší čísla umět sečíst / odečíst pod sebe na papíře – stránka o čítání a odčítání pod sebou je ZDE.

Samostatnou kapitolou je sčítání času. Schválně si někdy spočítejte, kolikrát si za den řeknete například „za hodinu půl se sejdeme…“ a v hlavě horlivě přičítáte k aktuálnímu času 1,5. Na to, jak se počítání času  často používá a jak je zvláštní (počítání s násobky 60/24/30 místo obvyklejších 100) se ve škole, podle mého názoru, málo procvičuje.

Násobení a dělení

Násobení je podle mě ještě důležitější než sčítání a odčítání. Nejen v obchodě. Například kolik mám koupit rohlíků, když je nás 5 a každý sní 3, kolik stojí 15 rohlíku, když 1 stojí 3 Kč, nebo kolik si můžu koupit limonád, když mám 100 Kč a jedna stojí 25 Kč atd. …
Velmi doporučuji dobře se naučit násobení a dělení násobky 10 (10, 100, 1000, 10000). Je to jednoduché (přidávají se nuly podle čísla, kterým násobíte) a použijete to poměrně často (počítání s penězi). Navíc vám to pomůže při odhadování přibližných výsledků.
Násobení a dělení potřebujeme v podstatě u každého z odstavců tohoto článku. U procent se násobí a dělí, u obsahů a objemů se bez něj taky neobejdete.

Desetinná čísla

Svět se neskládá jen z celých čísel, ale hlavně z desetinných. Máloco stojí 10 Kč, váží 3 kg nebo měří 1 metr. Spíš se potkáte s tím, že něco stojí 10,80 Kč, váží 3,2 kg a měří 1,82 m a právě s těmito čísly budete sčítat, násobit a počítat procenta.
Zase platí provázanost s ostatními odstavci. Sčítaní a odčítání, násobení a dělení ani procenta se bez desetinných čísel neobejdou. Desetinná čísla vysvětlujeme na této stránce.

Procenta

Podle mě jedna z nejdůležitějších věcí. Každý den se potkáváte s informacemi jako: inflace je 4 % (pominu jestli víte co je inflace), nezaměstnanost je 9%, hypoteční úrok je 3,5%, sleva je 30%, u těchto informací je potřeba si umět představit co počet procent vlastně znamená. Stojí 30% sleva na limonádu za 20 Kč za to, jet přes celé město do supermarketu?   60 % žáků třídy bylo proti, a to je prostě hodně = víc než polovina (víc než 50 %) = většina.
U počítání s procenty je potřeba si vždy uvědomit základ (100%), ke kterému se procentová část vztahuje. Často se třeba srovnávají výkony v jednotlivých letech. Např. prodej v obchodě oproti roku 2012 stoupl o 15 %, může to být napsáno i jako – letos jsme prodali 20680 knih a to je o 15 % víc než loni. V těchto příkladech je potřeba si uvědomit, že loňský rok je 100 % a od něho se počítá nárůst/pokles. Z hlavy byste měli umět počítat minimálně desítky procent (10%, 20%, 30%….). Nic na tom není (spočítáte 10 % – vydělíte základ 10 a vynásobíte 2,3,4…)  a  pomůže vám to se v procentech orientovat. Víte, že 50 % je polovina? 🙂

Zlomky

Se zlomky nebudete tak často počítat (sčítat , počítat složené zlomky,…). Je, ale nutné umět si představit kolik je 2/3, 1/10. Co je víc? Kolik je 1/3 třídy. A to nemluvím o základních 1/4 a 1/2. Často je v novinách např. „2/3 obyvatel nesouhlasí….“ nebo „desetina obyvatel nesouhlasí…“. V kterém případě víc lidí nesouhlasí?

Obvody a obsahy

Potřebujete spočítat kolik potřebujete barvy na vymalování pokoje, kolik semen koupit na osetí záhonku za domem, kolik vody je v sudu? Pak byste měli znát alespoň základní vzorečky pro počítání obsahů a objemů. Alespoň obdélník, kruh a kvádr musíte umět i o půlnoci, a to nejen jak vzorec zní, ale umět ho i používat.

Nechci tu popisovat další početní operace, které budete potřebovat. Bude samozřejmě záležet na vaší profesi. Ta vás v určitých operacích bude specializovat: prodavačka – sčítání odčítání z hlavy do tisíce, řemeslník – převody jednotek, obvody a obsahy, ekonom – sčítání a odčítání do miliónu a především procenta, atd. Nicméně nesmíte se ukolébat pomyšlením, že jiné operace pro vaši profesi nebudete potřebovat, platí to co je napsáno v odstavcích nahoře. Od všech těchto oblastí matematiky musíte znát minimálně základ.

Samostatně se zastavím u těch, kteří uvažujete o tom, že budete soukromě podnikat (v jakémkoli oboru podnikání). V tom případě musíte rozumět nejen oboru svého podnikání, ale i matematika bude pro vás moc důležitá. Nejen pro účetnictví (to pro vás může dělat externí firma), ale orientovat se v nákladech, schopnost určit správnou cenu, odhadnout výhodnost cenových nabídek se bez matematiky neobejde. Pokud tedy nechcete podnikat podle jednoho vtipu:

Potká profesor matematiky bývalého studenta Pepíka, který nebyl v matematice nejsilnější, a ze kterého se stal úspěšný podnikatel.
„Poslouchej Pepíku, tobě ta matematika moc nešla, jak to že se ti tak daří?“
„Ani nevím, pane profesore“ odpoví Pepík.“Koupím za 5 Kč, prodám za 10 Kč a těch  5% mi stačí“

Pokud vtip nechápete, tak honem na tyhle stránky a opakovat procenta.

A proto Vás moc prosím: snažte se umět matematiku – bude se Vám/nám všem dařit líp.

Budeme moc rádi, když se s námi podělíte o situace,kdy jste si uvědomili,že je pro Vás matematika důležitá. Pište do komentáře, nebo sem.