Na této stránce vám přineseme všechny informací k trojúhelníku, které budete na základní škole potřebovat. Najdete zde popis obecného trojúhelníku, rozdělení trojúhelníků (rovnostranný, rovnoramenný,…) a jejich zvláštnosti. Samozřejmě i řadu vzorců pro výpočet všeho co s trojúhelníkem souvisí (úhlů, výšek, atd.). Samostatně se pak budeme věnovat „králi trojúhelníků“ – trojúhelníku pravoúhlému.Tak pojďme na to…
Popis obecného trojúhelníku

Na obrázku vidíte obecný trojúhelník. Obecný trojúhelník píšeme proto, že nemá nic stejného (strany, úhly, výšky,…) ani nijak zvláštního (např. jeden úhel 90°).
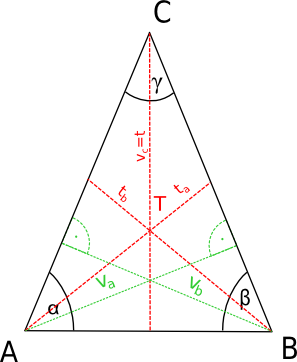
Trojúhelník je určen třemi body, kterým říkáme vrcholy trojúhelníka. V našem případě bodem A, B a C. Budeme ho tedy označovat jako trojúhelník ABC.
[pmath size=20]Delta ABC[/pmath]
Nemusí to být vždy ABC, klidně to může být ABH, CGK, MNO, OPR,… Vždy musí jít o tři různé body. Ne tedy AAB, PPM, ale A1A2A3 ano.
Každý trojúhelník má tři strany. V našem případě jsou to úsečky AB, BC a CA. Tyto úsečky se označují malými písmeny podle vrcholu (bodu) proti, kterému leží. Malé a bude úsečka BC, malé b je AC a malé c je úsečka AB. Samozřejmě pokud máte zadán trojúhelník MNO budou jednotlivé strany m, n, o.
Dále máme v trojúhelníku tři úhly (podle toho se jmenuje trojúhelník 🙂 ). Úhel u vrcholu A (mezi úsečkami AB a AC) se nazývá α (alfa), úhlu u vrcholu B (mezi úsečkami AB a BC) se říká β (beta) a úhel u vrcholu C (mezi úsečkami BC a CA) je γ (gama). U úhlů neplatí to co u stran. Označení úhlů se nutně neodvozuje od písmena bodu u kterého leží. I trojúhelník MNO může mít úhly α,β,γ a zároveň v trojúhelníku ABC mohou být úhly ε,λ,σ. Je potřeba pozorně sledovat zadání.
Výška trojúhelníku je úsečka, jejíž krajní body jsou: vrchol trojúhelníku (na našem obrázku C) a pata kolmice (C1) vedené vrcholem k přímce na níž leží protilehlá strana.
Zjednodušeně: výška je úsečka kolmá na stranu trojúhelníka, která vede do vrcholu ležícího proti této straně. Ta kolmost (úhel 90°) je moc důležitá!
A ještě obecněji: výška je vzdálenost rovnoběžek, kdy na jedné leží vrchol trojúhelníku a na druhé leží strana ležící proti tomuto vrcholu. Na našich obrazcích jsou to ty čárkované přímky.
Jak vidíte na obrázku vpravo nemusí být výška vždy uvnitř trojúhelníku, ale kolmice se vynese „mimo“ trojúhelník.

Těžnice trojúhelníku je úsečka, která spojuje vrchol a střed protilehlé strany. Těžnice se protínají v těžišti.
Kružnice opsaná se nazývá kružnice, která prochází všemi vrcholy tohoto trojúhelníku. Ke každému trojúhelníku lze sestrojit jen jednu opsanou kružnici. Střed kružnice opsané sestrojíme jako průsečík os stran (kolmice na stranu v jejím středu) a jak vyplývá z definice kružnice je vzdálenost všech vrcholů od středu stejná (r).

Kružnice trojúhelníku opsaná (střed je na průsečíku os stran)
Kružnice trojúhelníku vepsaná se dotýká všech stran trojúhelníku a její střed je průsečík os vnitřních úhlů (osa úhlu je přímka, která rozdělí úhel na dva stejné úhly). Vzdálenost středu od stran trojúhelníku je stejná.

Kružnice trojúhelníku vepsaná (střed leží na průsečíku os vnitřních úhlů)
Rovnostranný trojúhelník

– má všechny strany stejně dlouhé (shodné)
– všechny vnitřní úhly jsou shodné a mají velikost 60°
– všechny výšky a těžnice mají stejnou velikost -> těžnice je stejná jako výška
Obvod: o=3.aObsah: S=(a.va)/2
Rovnoramenný trojúhelník
– má shodné dvě strany (ramena). Třetí strana, která má jinou délku je základna.
– úhly při základně (alfa,beta) jsou shodné. Velikost neznáme, ale platí α = β = (180 – γ)/2
– výška k základně (vc) rozděluje základnu na poloviny.
Pravoúhlý trojúhelník
– má jeden vnitřní úhel pravý. To znamená jeden úhel má velikost 90°
– strany které svírají pravý úhel jsou odvěsny a třetí strana je přepona
– výška na jednu odvěsnu je totožná s druhou odvěsnou a naopak
– průsečík výšek splývá s vrcholem pravého úhlu
– rovnoramenný trojúhelník může být pravoúhlý
| druh trojúhelníku | délka stran | velikost úhlů | výšky | střed kružnice opsané |
| ostroúhlý | různé | všechny < 90° | protínají se uvnitř | leží uvnitř trojúhelníku |
| tupoúhlý | různé | jeden > 90° | se protínají mimo trojúhelníku | leží vně (mimo) trojúhelníku |
| rovnostranný | shodné | všechny = 60° | všechny shodné, totožné s těžnicemi | shodný s těžištěm i se středem kružnice vepsané |
| rovnoramenný | dvě shodné | dva shodné | výšky k ramenům jsou shodné | leží uvnitř trojúhelníku |
| pravoúhlý | (mohou být) dvě shodné | jeden = 90° (pravý) | dvě totožné s odvěsnami průsečík je vrchol pravého úhlu. | je středem přepony |
TEST NA PROCVIČENÍ ZNALOSTI O TROJÚHELNÍKU
| Více o matematice pro základní školy najdete například v těchto učebnicích. | ||
| Průvodce matematikou | Přehled matematiky | Přehled matematiky |
 |  |  |
| Podrobnosti | Podrobnosti | Podrobnosti |
| Na přijímací zkoušky vás připraví tyto učebnice. | ||
| TESTY 2018 český jazyk | Přijímací zkoušky z ČJ | Přijímací zkoušky na osmiletá gymnázia – Matematika |
 |  |  |
| Podrobnosti | Podrobnosti | Podrobnosti |
| Celá kategorie učebnic k přijímacím zkouškám. | ||
je to super
hodne mi to pomohlo.
A jak se sestrojí 3-úhelník, známe-li stranu a=8cm, úhel gama =60° a tc=6cm?
mil
Miloši, musíš jít na odpovědi a tam to opsat…
Hodne mi to pomohlo děkuju moc děkuju